Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Physics Quiz

Who is Who ?

Lagrange Applet (1)

A paper of N. Treitz inspired me to write this applet.

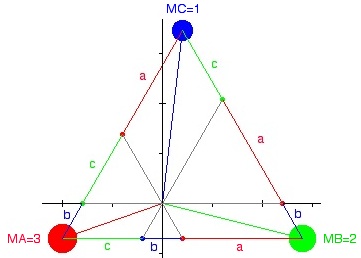
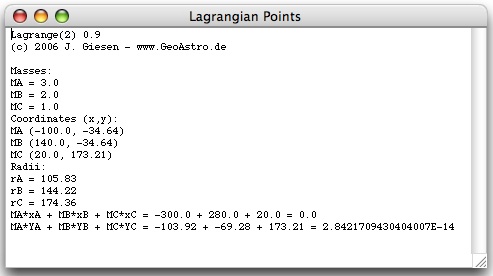
The applet is showing three bodies: mass MA at (xA,yA) mass MB at (xB,yB) mass MC at (xC,yC) forming an equilateral triangle. The center of mass is at (0,0). MA*xA+MB*xB+MC*xC = 0 MA*yA+MB*yB+MC*yC = 0

The lengths of the segments a, b, c are proportional to the value of the masses MA, MB, and MC. The positions of a, b, and c are opposite to the corresponding mass.

	Select from the view options of the menu.
	You may use the key "r", or "R" (shift key and "r", faster) to rotate the system around the center of mass. Click the applet first ! Select "Reset" to return.

Web Link

N. Treitz: Trojaner am Himmel, Spektrum der Wissenschaft, Oktober 2006 The Lagrange Points The Lagrange Points Effective Potential and the Lagrangian Points Gravitation Simulations The Lagrangian Points for a Planetary Orbit Lagrangian point (wikipedia) Gaia's Lissajous Type Orbit Klemperer Rosettes Satellite in the triangular libration point (example 7) Lagrange points for two similar masses Satellites Click, drag and release to set location, speed and direction. Try to manage a Lagrange point! Orrery: Solar System Simulator

Updated: 2006, Oct 07