GeoAstro
Applets
Astronomy
Chaos Game
Java
Miscel-
laneous
|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
 |
Use the checkboxes (at
the left or right) to select one of the two cases of q. |
  |
Checking the box will
mark certain values of p (right axis) - p is a multiple of the raster size, and - the roots x1 and x2 are multiples of the raster size. |
 |
Select the
raster size, or a continuous mode ("Raster off"). A table of p, q, x1, x2 is available by "Data Window". |
| The Greeks
created a geometric algebra: terms of equations were
represented by sides of geometric objects, usually
lines, and found by constructive methods. The method in my applets is presented in the paper of Hornsby. It is based on Euclid's Elements, Book II, Proposition 11, and Book VI, Propositions 28 and 29. 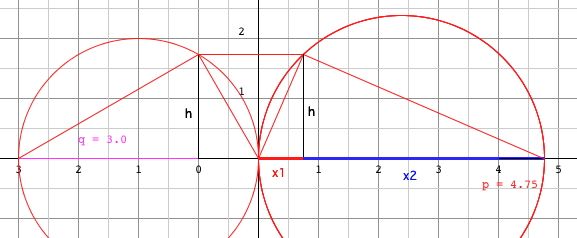 Using the
Right Triangle Altitude Theorem
(Altitude-On-Hypotenuse Theorem):
q·1 = h2
and x1·x2 = h2
x1·x2 = q and x1·x2 = |p| (Vieta) |
