|
The motions of Earth and planets are usually computed in ecliptic coordinates, based on the plane of the ecliptic. The position of an object is defined by the ecliptic latitude (=0 for the sun), the ecliptic longitude, and the distance. The figure represents the elliptical orbit of a body K, the Sun situated in the focus S: 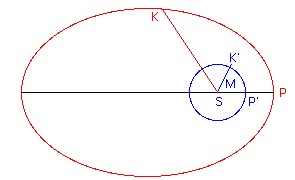 We consider a fictitious body K' describing a circular orbit around S with constant velocity, with the same period as the real body K, and situated at P' at the instance when the real body is at the perihelion P. The angle PSK' is called mean anomaly M, increasing linearly with time. The problem consists in finding the true anomaly (angle PSK) at a given instant, when the mean anomaly M and the eccentricity of the ellipse are known.
Julian Day (valid from 1900/3/1 to 2100/2/28) Julian day: 86400 s, Julian year: 365.25 d, Julian Century: 36525 d double JulianDay (int date, int month, int year, double UT) { if (month<=2) {month=month+12; year=year-1;} }
Solar Coordinates (according to: Jean Meeus: Astronomical Algorithms), accuracy of 0.01 degree k = 2*PI/360;
convert
ecliptic longitude L to right ascension RA
and declination delta // number of Julian centuries since Jan 1, 2000, 12 UT
compute sidereal time at Greenwich (according to: Jean Meeus: Astronomical Algorithms) T = (JD - 2451545.0 ) / 36525
convert tau, delta to horizon coordinates of the observer (altitude h, azimuth az): sin h = sin(latitude)*sin(delta) + cos(latitude)*cos(delta)*cos(tau)
Home back to "Positional Astronomy" "Sun, Moon & Earth Applet"
|