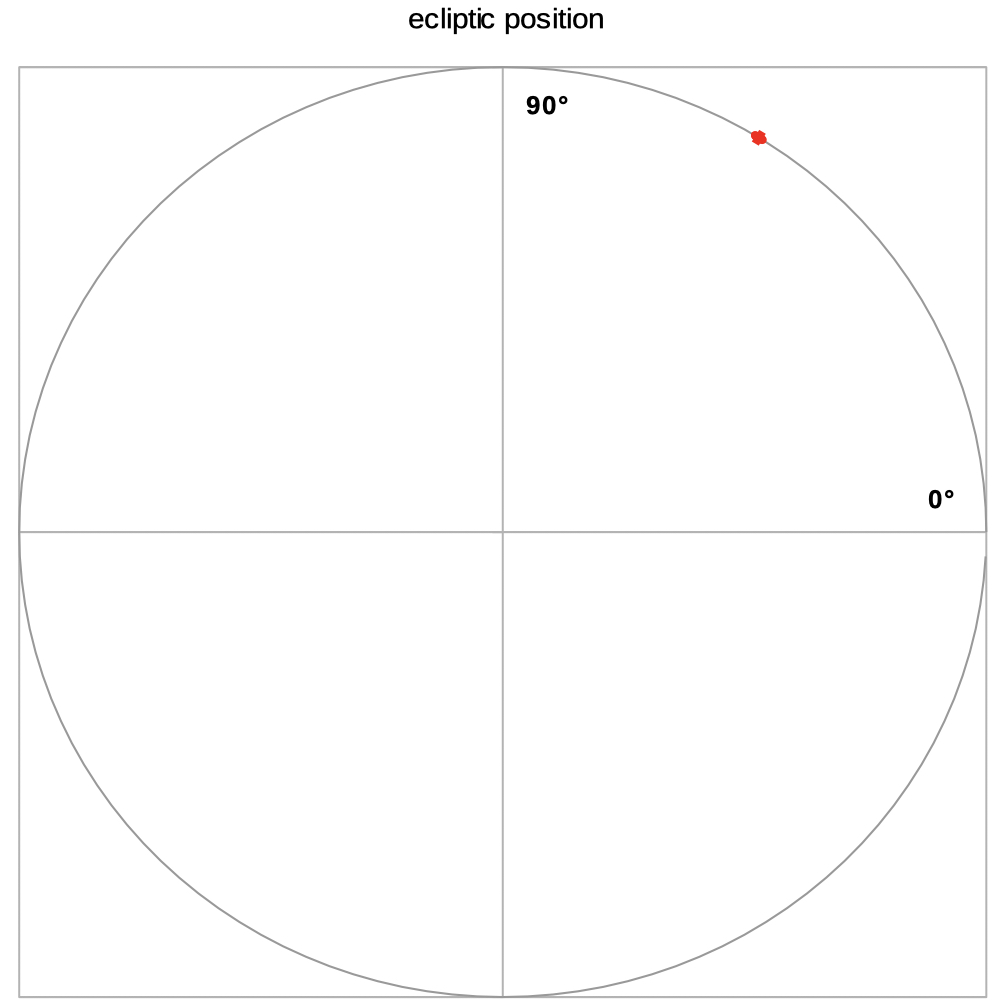
Position of the Moon
START
the Sun for a month the Sun for a year
Position of the Sun by
Spreadsheet
for a day
download
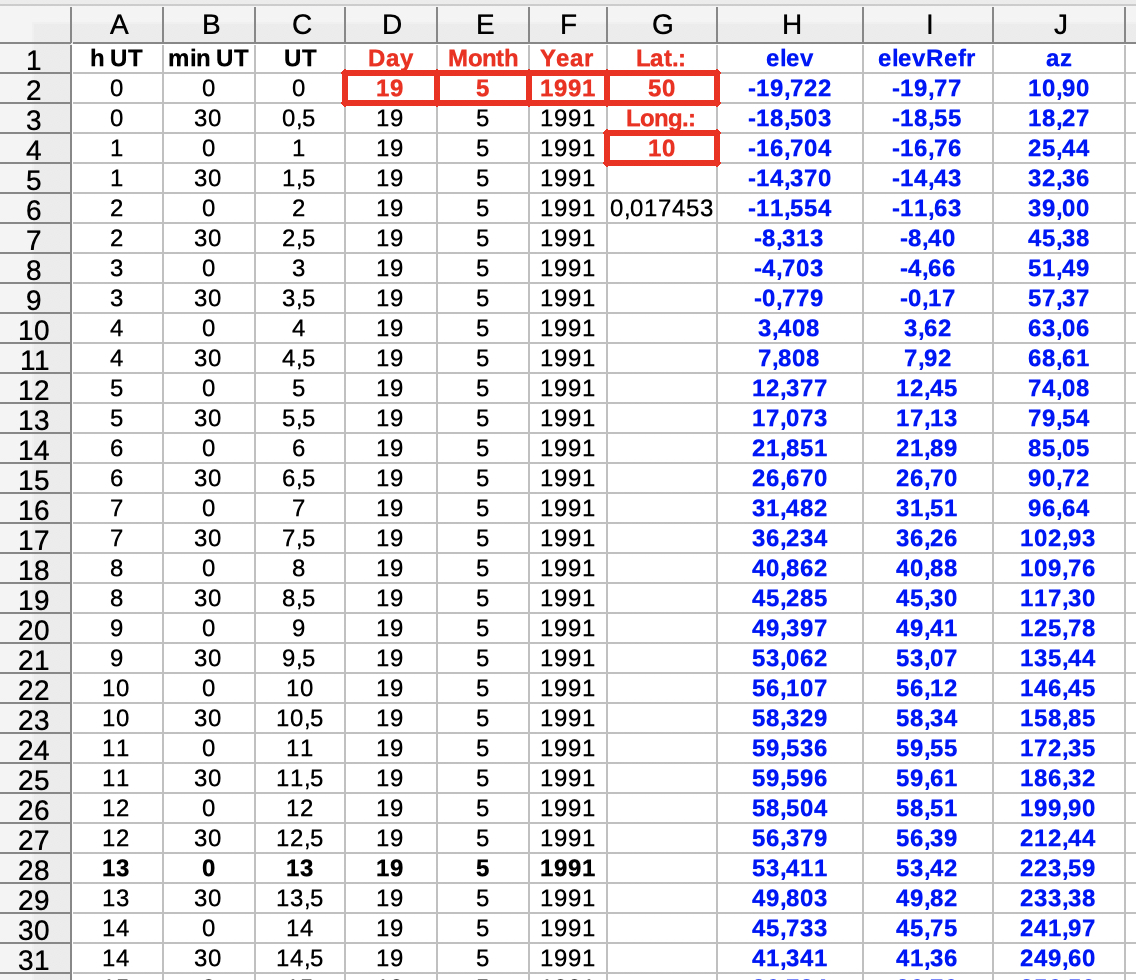
| Select the
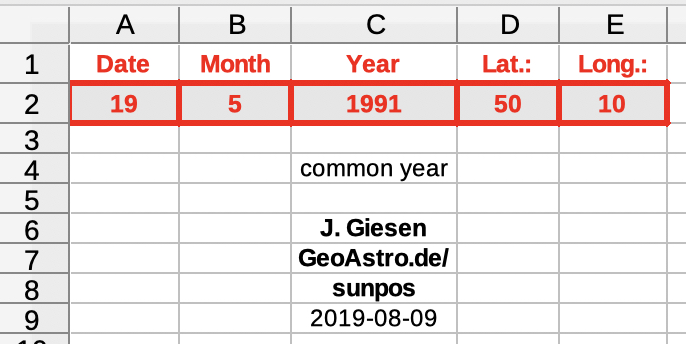
table 'input': |
|
|
Input (red frames): 1) date, month, year Don't modify any other cells. |
 |
| The table calc
performs the calculations, using a lot of auxiliary
variables. It should be neglected. |
|
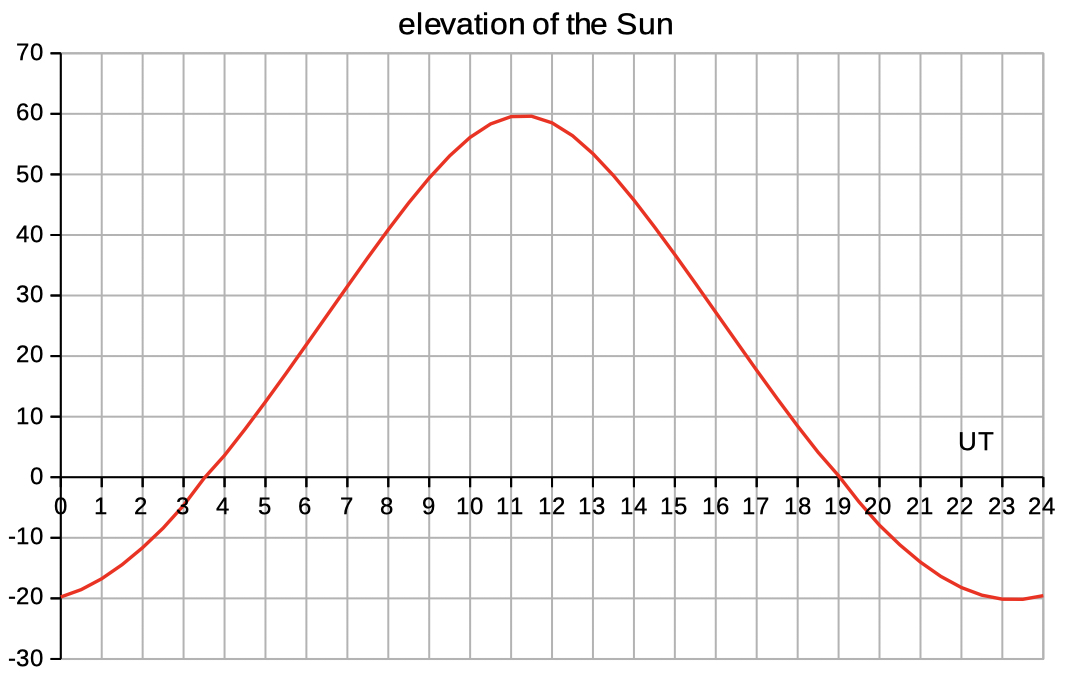
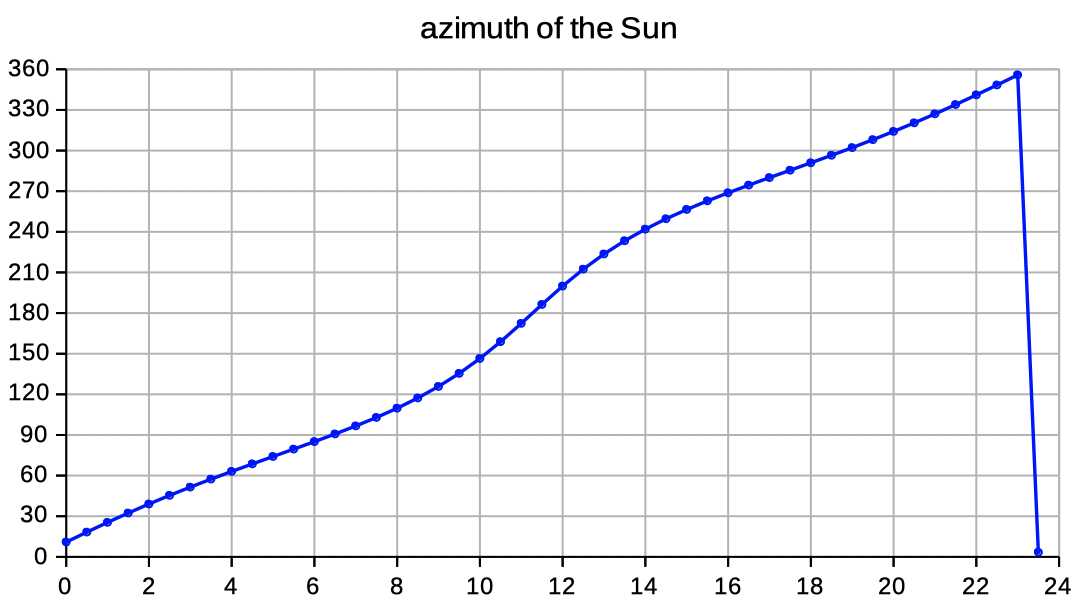
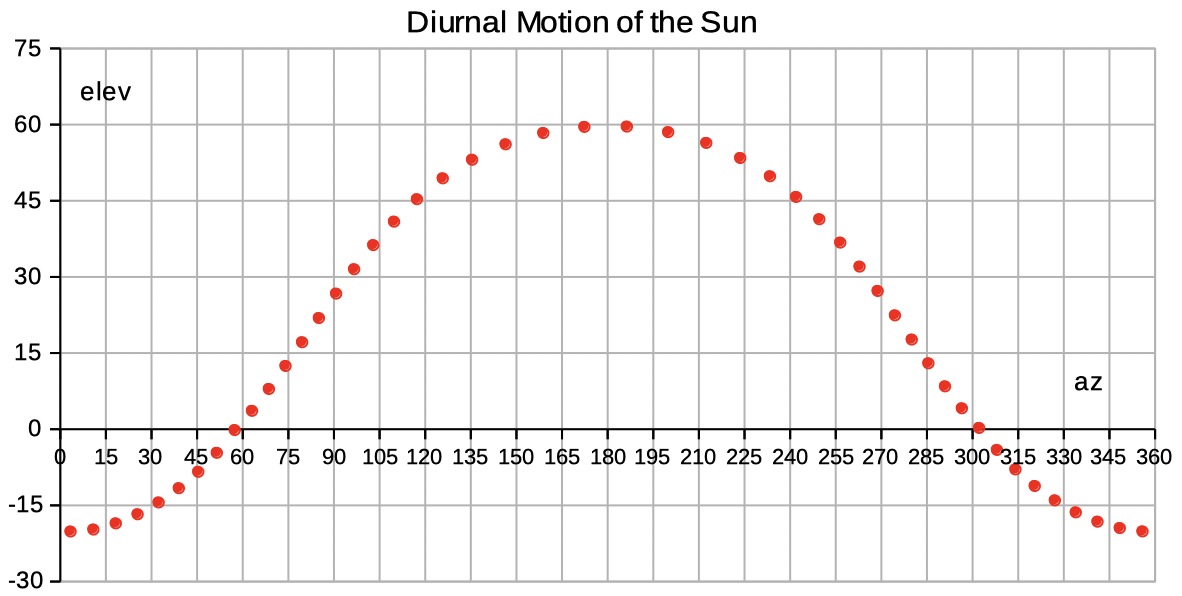
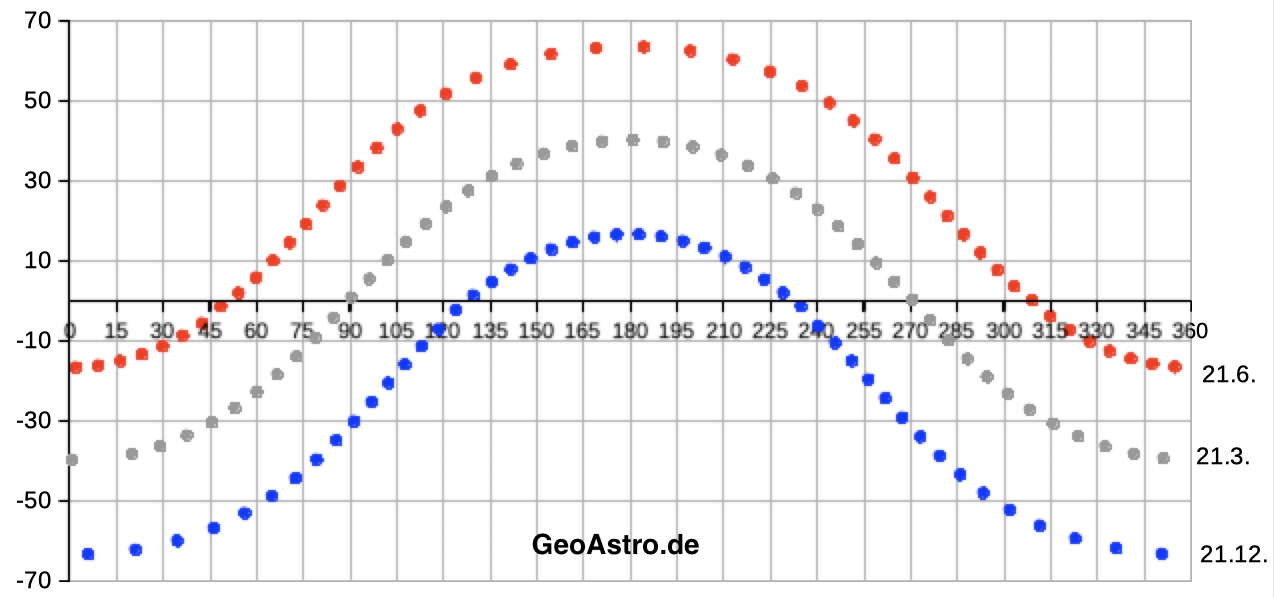
| Select elev az to see data and diagrams of elevation and azimuth. | |
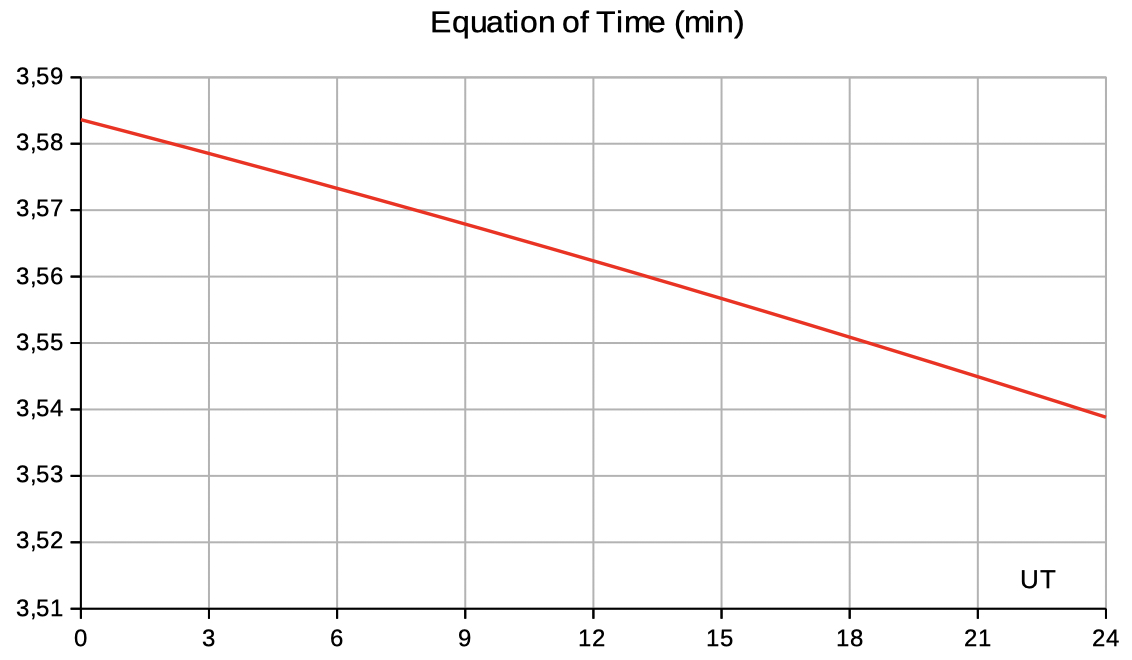
| Select E o T for
data and diagrams of the Equation of Time. |
|
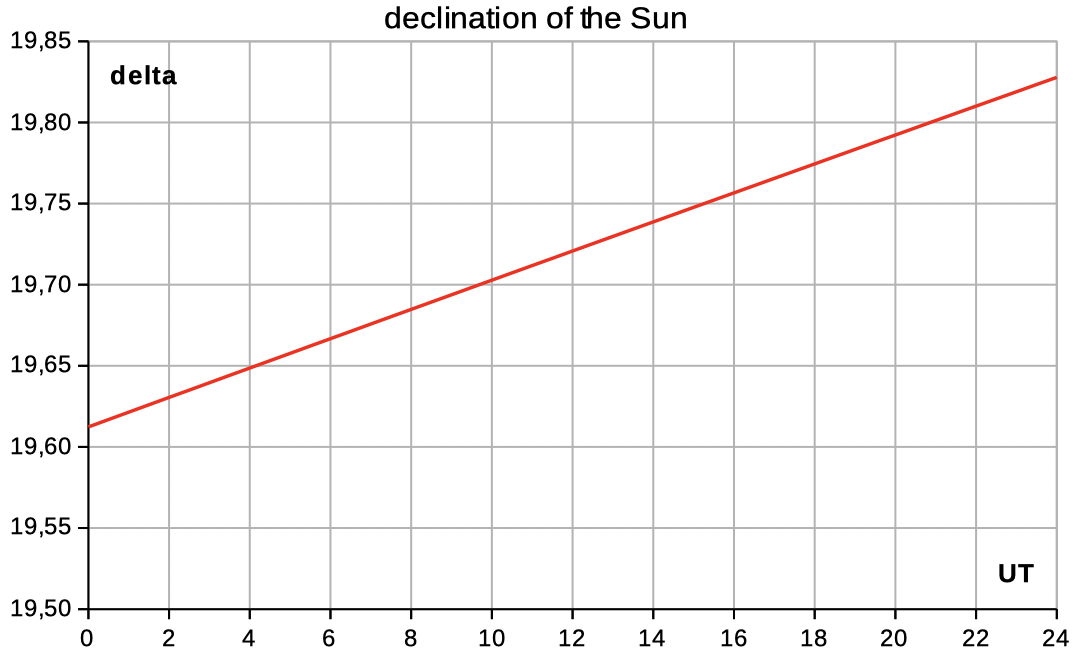
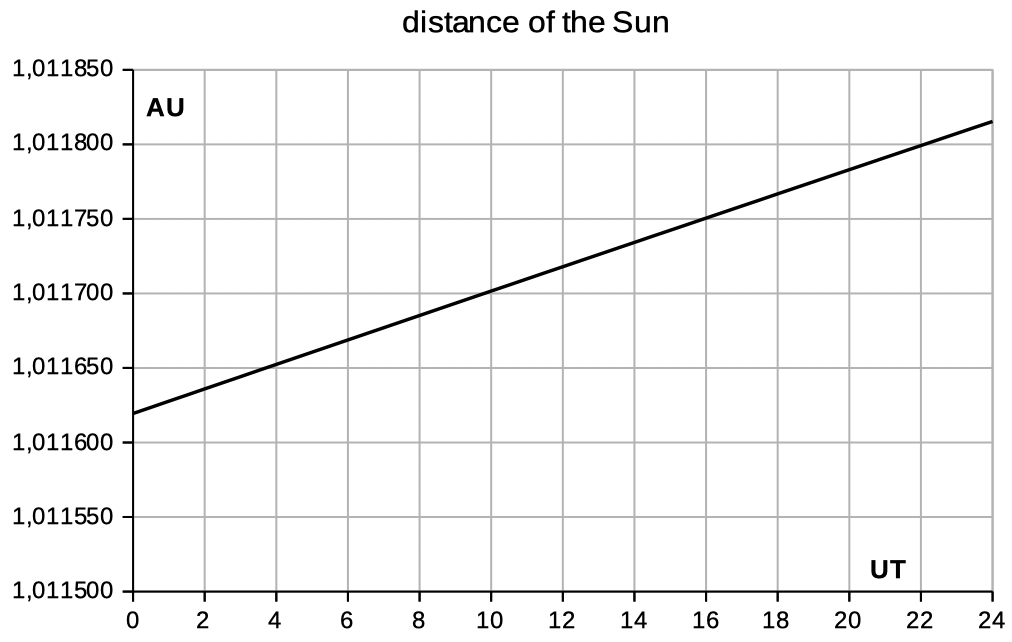
| Select declin
dist to see data and diagrams of the
declination and distance. |
|
| Select orbit to see data and a diagram of the ecliptic orbit. |